Machine learning approaches in climate modelling
Doctoral Researcher:
Sonal Rami, Alfred Wegener Institute Helmholtz Centre for Polar and Marine Research, Bremerhaven, sonal.rami@awi.de
Supervisors:
- Prof. Dr. Thomas Jung, Alfred Wegener Institute Helmholtz Centre for Polar and Marine Research, Climate Dynamics, Bremerhaven, Thomas.Jung@awi.de
- Prof. Dr. Peter Maaß, University of Bremen, Department of Mathematics and Informatics, Center for Industrial Mathematics, pmaass@uni-bremen.de
Location: Bremen/Bremerhaven
Disciplines: climate dynamics, applied mathematics, computer science
Keywords: climate modelling, machine learning, exascale-readiness
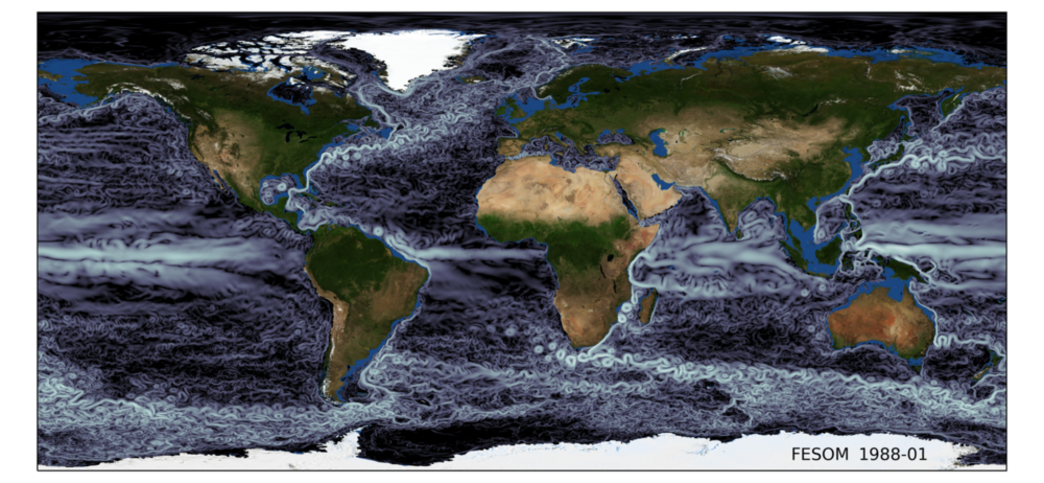
Motivation: Computer simulations cannot fully resolve the full dynamics of the real world—there will be always a need for spatial and temporal discretization that will require parameterization of the scales that are smaller than the discretization scale. These parameterizations are usually obtained from a limited number of observations that are not necessarily representative for the whole globe, and often heavily tuned in order to obtain a final solution that is close to the observed mean state of the climate system. Machine learning (ML) methods allow the development of parameterizations that can outperform classical methods, providing much more robust solutions (e.g. Reichstein et al, 2019 and references therein). In this context, one of the main challenges—touching both the marine (physics) and the computer science domain—is to constrain these parameterizations by physical laws, so that the main conservation principles are not violated. Furthermore, sea ice-ocean models such as FESOM have certain bottlenecks in high-resolution configurations that seriously inhibit scalability—and thus effective use of next-generation exascale supercomputers. In this context, it has been suggested that replacing computationally expensive parts by machine learning approaches will help to making models exascale-ready.
Aim: In this project, two main hypotheses will be tested: (1) Machine learning will lead to much better parametrizations in climate models and (2) machine learning methods can help to overcome computational bottlenecks in high-resolution model runs on extreme-scale high-performance computers. Firstly, it is planned to develop new parameterizations for representing ocean eddies in the Finite Volume Sea Ice-Ocean Model (FESOM2), which has been developed at AWI. To this end, models that explicitly resolve eddies at ultra-high resolution will be used as examples to train the ML model. Furthermore, observational knowledge will be entrained as well. Secondly, it is planned to go one step further by using ML methods for replacing certain parts of Earth system models that present computational bottlenecks for high-resolution configurations. In this context, a good candidate is the sea ice model. As a first step, it is planned to try training the ML model on the same or high-resolution version of the same sea ice model taken as a “true” solution. Furthermore, it is planned to examine how satellite observations can be integrated in the ML model. In general, the integration of additional domain specific information given as data (e.g. satellite data) or physical models (e.g. for describing the basic physical laws of ice formation) requires specific network structures and adapted training procedures. Here, we aim in particular at obtaining very high-resolution models, where the underlying mathematical model leads to an ill-posed inverse problem. This requires adapting regularized deep learning approaches based on generative adversarial network architectures (Arridge et al. 2019).
Objectives: (1) Improve the realism of climate models and hence their ability to project future climate change, (2) develop parametrizations of subgrid-scale processes based on ML methods for FESOM2, and (3) overcome computational bottlenecks in FESOM2 by replacing part of the code by ML approximations.
References:
- Arridge, S., P. Maass, O. Öktem and C. Schonlieb, 2019: Machine learning for solving inverse problems. Acta Numerica.
- Reichstein, M., et al. 2019: Deep learning and process understanding for data-driven Earth system science. Nature, 566, 195–204.